Materi TIU - Persamaan dan Pertidaksamaan

Hai sobat elpedia, salam sukses tetap semangat belajar! Pada halaman ini kita akan meringkas materi seputar Persamaan dan Pertidaksamaan. 

A. Persamaan
perlu sobat elpedia ketahui bahwa persamaan terbagi menjadi: persamaan linier (1 variabel, 2 variabel, 3 variabel) dan persamaan kuadrat.

1. Persamaan Linier 1 Variabel
bentuk umum sebagai berikut :

ax + b = c

di mana:
a, b = konstanta
x     = variabel (peubah)

sobat elpedia perlu ketahui variabel x dapat dicari dengan cara sebagai berikut:
ax + b = c  =>  ax = c - b

2. Persamaan Linier 2 Variabel
Bentuk umumnya sebagai berikut :

ax + by = c

dimana:
a, b, c = konstanta
x, y     = variabel

3. Persamaan Linier 3 Variabel
bentuk umum dari persamaan linier 3 variabel :

ax + by + cz = d

dimana:
a, b, c, d = konstanta
x, y, z     = variabel

Sobat elpedia, untuk menyelesaikan persamaan linier 3 variabel dibutuhkan minimal 3 buah persamaan. variabel x, y, dan z dapat di cari dengan menggunakan cara Eliminasai dan Subtitusi.

4. Persamaan Kuadrat
bentuk umumnya :

ax² + bx + c = 0

dimana:
a, b, c   = bilangan riil
a           ≠     0
x ₁, x ₂ = akar-akar Persamaan Kuadrat
             = pembuat nol
             = penyelesaian Persamaan Kuadrat

Perlu diketahui, ada 3 cara untuk mencari akar-akar persamaan kuadrat:

1. Cara faktorisasi
2. Cara melengkapkan bentuk kuadrat
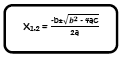
3. Rumus ABC

B. Pertidaksamaan
perlu sobat elpedia ketahui bahwa pertidaksamaan adalah kalimat matematika terbuka yang mengandung simbol:  > , < , ≤  atau ≥ 

sifat-sifat pertidaksamaan
jika a>b, maka dapat kita ambil sifat:

1. a + c >  b + c
2. a - c  >  b - c
3. a x c  >  b x c    ==> untuk c = positif
4. a x c  <  b x c    ==> untuk c = negatif
5. a : c   >  b : c    ==> untuk c = positif
6. a : c   <  b : c    ==> untuk c = negatif

Jenis-jenis pertidaksamaan antara lain:
a. Pertidaksamaan Linier
bentuk umumnya:

ax + b > c

langkah-langkah untuk menyelesaikannya:
pindahkan b ke ruas kanan
kurangkan c dengan b
kedua ruas di bagi dengan a

b. Pertidaksamaan kuadrat
bentuk umumnya:

ax² + bx + c > 0
ax² + bx + c < 0

langkah-langkah untuk menyelesaikannnya:
cari akar-akar persamaan kuadrat
diperoleh x₁ dan x₂ (misalnya : x₁ <  x₂ )

jika tanda pertidaksamaan ">"
maka : x < x₁ atau x > x₂

jika tanda pertidaksamaan " < "
maka : x₁ < x < x₂